De theorie van de Utrechtse Nobelprijswinnaars

Het standaardmodel van de wisselwerkingen die elementaire deeltjes onderling aangaan, beschrijft de vier natuurkrachten (de sterke kracht, de elektromagnetische kracht, de zwakke kracht, en de zwaartekracht) door middel van drie zogenaamde niet-abelse ijktheorieën, waarover later meer. De elementaire deeltjes van het standaardmodel zijn zes leptonen en zes quarksmaken, waarbij elk van de quarksmaken kan voorkomen in drie kleuren.

Om de essentiële bijdrage van de beide gelauwerde hoogleraren aan het standaardmodel enigszins te verduidelijken, moeten eerst wat algemene begrippen uitgelegd worden. Het standaardmodel beschrijft de fundamentele deeltjes en hun krachtdeeltjes met de kwantumveldentheorie. Kort gezegd betekent dit dat ieder elementair deeltje zijn eigen veld heeft waarvoor wiskundige veldvergelijkingen opgesteld kunnen worden. Overigens gaat de in deze eeuw ontwikkelde kwantummechanica op vele fronten tegen het gezonde verstand in. Rondom de kleinste deeltjes is een fundamentele onzekerheid komen te hangen. Zo toonde de geniale Heisenberg in 1925 aan dat het onmogelijk is om zowel de plaats als de snelheid van een subatomair deeltje te weten (het onzekerheidsprincipe van Heisenberg). Gelukkig is dit bij 'gewone', dus grotere, objecten niet te merken, en kunnen plaats en snelheid van een tennisbal of een ruimtevaartuig nauwkeurig berekend worden.

De huidige deeltjestheorieën van het standaardmodel zijn dus de al eerder genoemde ijktheorieën. Dit zijn theorieën die tonen hoe krachten kunnen ontstaan vanuit onderliggende symmetrieprincipes, en de wiskunde van symmetrieprincipes wordt groepentheorie genoemd. Zonder op de details in te gaan, is het zo dat je bijvoorbeeld een constante aan een bepaald systeem van deeltjes mag toevoegen, zonder dat het eindresultaat (welke deeltjes ontstonden er, hoeveel en in welke richting?) verandert. Met andere woorden: de symmetrie blijft behouden doordat de natuurwetten blijven gelden. Een verandering die we in zo'n systeem kunnen aanbrengen heet een ijktransformatie. Als aan de eis van onveranderlijkheid voldaan wordt, spreken we van ijkinvariantie.

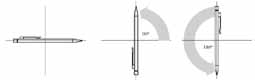
We gaan nu enkele ijktransformaties na elkaar uitvoeren, die we A en B noemen. Bij een abelse transformatie maakt het niet uit of we eerst A doen en dan B, of omgekeerd. Elektromagnetisme is bijvoorbeeld een abelse ijktheorie. De elektromagnetische kracht, opgesteld door James Clerck Maxwell in 1873, is een schitterend voorbeeld van de samenvoeging van natuurkrachten. Maxwell ontwikkelde namelijk een theorie waarin de elektrische en de magnetische krachtvelden samengevoegd bleken te kunnen worden tot één kracht. Bij een niet-abelse transformatie maakt het wel uit in welke volgorde je het doet. Eerst A en dan B is dan niet hetzelfde als eerst B en dan A. Probeer het maar eens met een pen:

De belangrijkste eis van een goede ijktheorie is dat het niet mag leiden tot onzinuitkomsten. Deze voorwaarde lijkt logisch, maar een wiskundige onderbouwing waardoor absurde uitkomsten, zoals onverklaarbare 'oneindige' uitkomsten, vermeden kunnen worden, is nog niet zo eenvoudig. Pas als een deeltjestheorie een gedegen wiskundig fundament bezit, kunnen er bruikbare en nauwkeurige berekeningen gedaan worden. Het eerste geslaagde voorbeeld van zo'n ijktheorie was de kwantumelektrodynamica (QED).

In de QED gehoorzamen de elektrische en de magnetische velden aan de wetten van de kwantummechanica. Tussen 1925 en 1940 werkte de QED echter niet goed omdat er uit de berekeningen steeds ”oneindig” als antwoord uitkwam. Waarom? De reden is dat je niet zomaar aan een ”kaal” elektron kunt gaan rekenen. Volgens de kwantumtheorie geldt dat als je een ”kaal” elektron onder een loep zou kunnen bekijken, je een ”wolk” van extra deeltjes (bijvoorbeeld fotonen) ziet.

De omringing van een elektron door al die virtuele deeltjes geeft allerlei wiskundige problemen. In 1940 werd dit probleem op een briljante wijze opgelost door Tomonaga, Schwinger en Feynman (deelden de Nobelprijs in 1965). De oplossing bestond uit het renormeren van de theorie. Dit is een wat ingewikkeld begrip. In feite houdt het in dat het elektron van een ”afstandje” bekeken wordt waardoor een ”aangekleed” deeltje wordt gezien. In de berekeningen wordt hier vervolgens rekening mee gehouden. Uiteraard zien we in het experiment ook nooit een ”kaal” elektron. Een theorie is pas renormeerbaar als het ”aangeklede” deeltje dezelfde natuurkundige wetten volgt als het ”naakte” deeltje onder de microscoop.

Samenvattend: de genoemde natuurkundigen renormeerden een abelse ijktheorie.

Dat de QED een zeer nauwkeurig model is, blijkt uit het feit dat de eigenschappen van een elektron tot wel negen cijfers achter de komma berekend kunnen worden.Omdat deze aanpak de QED zo goed lukte, lag het voor de hand om te proberen ijktheorieën voor de andere natuurkrachten op te stellen. In de tweede helft van de jaren zestig slaagden Glashow, Salam en Weinberg erin de elektromagnetische en de zwakke kracht samen te voegen in een niet-abelse ijktheorie. Als krachtdeeltjes werden de W- en Z-deeltjes voorspeld, de zogenaamde vectorbosonen.

Er bleek niets nieuws onder de zon te zijn want vergelijkbare wiskundige problemen traden op. Berekeningen om de eigenschappen van W- en Z-deeltjes te bepalen werden opnieuw geplaagd door absurde oneindige uitkomsten. Dit probleem hield vele fysici op de wereld bezig.

De Utrechtse hoogleraar Veltman wilde het echter eens anders gaan aanpakken en greep hiervoor een oudere ijktheorie uit de kast: de Yang-Mills-theorie. Deze niet-abelse Yang-Mills-theorie uit 1954 was eigenlijk een uitgebreidere versie van het elektromagnetisme, met meer toegestane ijktransformaties en ook meer deeltjesvelden. De meeste deeltjesfysici waren nogal sceptisch over de bruikbaarheid van de theorie, maar Veltman bleef volhouden dat er tenminste iets van dit model goed moest zijn.

In de originele Yang-Mills-theorie hadden de krachtdeeltjes echter geen massa, en er moest wel een massa in voorkomen wilde de ijkinvariantie van de theorie overeind blijven. Daarnaast moest de nieuwe ijktheorie ook nog eens renormeerbaar zijn. De berekeningen bleken helaas enorm complex te zijn. Zou de theorie wel te renormeren zijn?

Tussen 1966 en 1970 kwam Veltman al een heel eind, maar de uiteindelijk klus werd boven alle verwachting geklaard door Veltman's jonge promovendus Gerard 't Hooft. De lastige oneindigheden vielen allemaal tegen elkaar weg. In twee publikaties toonde 't Hooft aan dat een renormeerbare niet-abelse ijktheorie van de zwakke kracht mogelijk was en een zinvolle beschrijving kon leveren van de werkelijkheid. Dat werd later onomstotelijk bewezen met de ontdekking van de W- en Z-deeltjes op het CERN in 1983. De massa van de top-quark kon bijvoorbeeld ook met grote nauwkeurigheid berekend worden.

Gerard 't Hooft heeft de periode van dertig jaar terug ooit de „glorieuze jaren zeventig” genoemd. Temeer, omdat in deze tijd ook een niet-abelse ijktheorie voor de sterke kracht, de kwantumchromodynamica (QCD), opgesteld kon worden (de krachtdeeltjes die de kleurkracht dragen zijn acht massaloze gluonen, zie figuur 1).

Noodzakelijk voor de wiskundige geldigheid van de theorieën is het bestaan van het Higgs-deeltje. Dit Higgs-deeltje (genoemd naar P. W. Higgs van de universiteit van Edinburgh) zorgt ervoor dat quarks en leptonen een massa hebben, oftewel het geeft antwoord op de vraag waarom er überhaupt massa is. Ondanks dat het deeltje nog nooit experimenteel is aangetoond, is zijn bestaan zeker. Anders zou de elektrozwakke theorie immers niet te renormeren zijn. Naar dit voortvluchtige deeltje wordt naarstig gezocht, maar het zal alleen bij verschrikkelijk hoge energieën in de deeltjesversneller kunnen ontstaan. De hoop is daarom gevestigd op een nieuwe deeltjesversneller, de Large Hadron Collider (LHC) die op het CERN in aanbouw is.

En hoe nu verder? Het samenvoegen van natuurkrachten in één fundamentele kracht vormt nog steeds de ultieme uitdaging van fysici. Deze alomvattende theorie zou dan volledig moeten verklaren waarom de materie in het heelal is opgebouwd zoals ze is opgebouwd. Velen proberen een dergelijke ”Theorie van Alles” te vinden. Voor drie krachten is dit al gelukt, maar het grote probleem is nog steeds de zwaartekracht. Deze voor ons meest vertrouwde kracht, is in verhouding tot de andere krachten een ongelofelijke zwakke kracht, maar zorgt er ondertussen op macroscopische schaal wel voor dat alles naar het aardoppervlak toevalt en dat planeten in hun baan rond de zon blijven.

Het rekenen aan de zwaartekracht is echter verschrikkelijk moeilijk, en deze kracht 'past' op het niveau van de elementaire deeltjes niet in het keurslijf van het Standaardmodel. Dit komt omdat de principes van de kwantummechanica niet goed te verenigen zijn met de zwaartekracht. Het bekende probleem van de oneindige uitkomsten treedt op, zodat al deze onrenormeerbare theorieën vooralsnog schipbreuk lijden. Een zeer revolutionaire aanpak zal nodig zijn deze hindernis te overwinnen, alhoewel er natuurkundigen zijn die ervan uitgaan dat de zogenaamde snarentheorie, waarin elementaire deeltjes geen puntjes maar trillende lijntjes zijn, de zwaartekracht met de kwantummechanica al heeft verzoend.

Het meer recente werk van 't Hooft heeft dan ook betrekking op het vinden van een oplossing voor deze nieuwe uitdaging. Hij is er echter nog niet van overtuigd dat de snarentheorie de alomvattende theorie is. Daarom rekent hij aan piepkleine zwarte gaten. Een zwart gat is een ruimte-tijd object met een zeer grote dichtheid. Doordat een zwart gat het allersterkste zwaartekrachtveld heeft dat mogelijk is, kunnen zelfs lichtstralen er niet uit ontsnappen! Volgens de relativiteitstheorie van Einstein kunnen ruimte en tijd in steeds kleinere delen worden gesplitst, maar moderne fysici denken dat de werkelijkheid eerder is opgebouwd uit hele kleine blokjes die minimaal 10-35meter groot zijn: dus 0.00000000000000000000000000000000001 meter.

Een probleem bij die immens kleine afstand is dat er allerlei natuurkundige problemen ontstaan doordat de kromming van de ruimte (volgens Einstein zorgt de zwaartekracht voor een kromming van de ruimte-tijd) heel erg groot wordt. Een kleinere lengte bestaat er volgens de theorie niet, en het gevolg is dat ruimte en tijd bij die afstand gaan verfrommelen.

Volgens 't Hooft kan daar de oplossing wel eens liggen, namelijk in het feit dat er bij 10-35meter piepkleine zwarte gaten zouden ontstaan. De filosofie van 't Hooft is dat het gedrag van een zwart gat misschien de sleutel vormt om de tegenstelling van de kwantummechanica en de zwaartekracht op te heffen, alhoewel hij met deze opvatting vrijwel alleen staat in de wereld van zijn collegae.

Omdat zwarte gaten haaks staan op de regels van de kwantummechanica is volgens 't Hooft het laatste woord nog niet gezegd over de kwantummechanica. Het is bekend dat Einstein van de kwantummechanica zelf niets moest hebben, maar de pogingen van de grote geleerde om de onjuistheid hiervan aan te tonen, faalden echter. Die moeite heeft blijkbaar ook 't Hooft heeft met de kwantumtheorie zoals die er momenteel uitziet. Vele fysici beschouwen 't Hooft echter als een buitenbeentje vanwege zijn ideeën over dit fundament van de hedendaagse natuurkunde.

Houdt de fysica ooit op? Voorlopig is deze vraag niet te beantwoorden en kunnen natuurkundigen hierop hun tanden nog stukbijten. Welke diepere structuurlagen van de materie zullen er nog te ontdekken zijn? De ontwikkeling van nauwkeurige deeltjestheorieën heeft namelijk ook een financiële kant: bouwen we wel of geen nieuwe miljarden dollars verslindende deeltjesversnellers om nieuwe exotische deeltjes te ontdekken? Mocht een ”Theorie van Alles” gevonden worden, dan zal de wereld echter gewoon doordraaien. Het zal dan alleen duidelijk zijn welk een ongelofelijk schone ordening er aan de geschapen werkelijkheid ten grondslag ligt. Vooralsnog gaat de speurtocht, waar de Oude Grieken al mee begonnen, nog steeds door. Alleen kon Democritus van Abdera nooit hebben vermoed dat zijn 'atomen' in werkelijkheid een miljoen keer zo klein waren als de zandkorreltjes die aan zijn voetzolen bleven hangen.

Aanbevolen literatuur:

Goede toegankelijke boeken zijn twee populair-wetenschappelijke boeken:

De bouwstenen van de schepping, Gerard 't Hooft, Ooievaar pocket, Amsterdam, 1994.

Dromen over een alomvattende theorie, Steven Weinberg, Uitgeverij Contact, Amsterdam, 1993.

Voor de wat meer ingewijden zijn de volgende artikelen aan te bevelen:

Gauge Theories of the Forces between Elementary Particles, Gerard 't Hooft, Scientific American, juni 1980, p. 90-116.

The Higgs boson, Martinus J.G. Veltman, Scientific American, november 1986, p. 88-94.