Spin en vlieg laten hersens kraken
Door S. M. de Bruijn
Op een tafel staan twee even grote glazen. Het ene is bijna helemaal gevuld met water, het andere is halfvol met wijn. Met een vingerhoedje breng je wat water uit het ene glas in het glas wijn, je mengt het en daarna breng je een vingerhoedje wijn –met iets water erin– over in het glas water. Zit er nu meer water in het glas met wijn dan wijn in het glas met water?
Dit is typisch zo'n hersenkraker die uitnodigt om te gaan rekenen. Stel dat er 80 milliliter water in het ene en 40 milliliter wijn in het andere glas zit en het vingerhoedje is 2 milliliter, dan zit er uiteindelijk in het waterglas 78 + 0,095 milliliter water + 1,905 milliliter wijn .... Na vijf minuten rekenen kom je tot de verrassende conclusie: Er zit evenveel water in het glas met wijn als wijn in het glas met water. Logisch, de inhoud van de glazen is uiteindelijk niet veranderd: wat er bij het ene glas uitgaat, komt terecht in het andere en omgekeerd.
Iedereen kent het raadsel van de vier lucifers en het schepje puin, of van de boer die een wolf, een kool en een geit moet overvaren. Maar wie op een verjaardag eens met een originele breinbreker wil aankomen, schaffe het boekje ”De spin en de vlieg” aan, geschreven door H. Ligtenberg, natuurkundedocent aan het Ichthuscollege in Veenendaal.
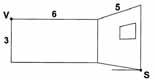De bundel met 125 raadsels ontleent zijn titel aan een kamer van 6 bij 5 bij 3 meter (lxbxh, zie afbeelding). In de hoek rechtsonder zit een spin. Precies daartegenover, in de hoek linksboven, zit een vlieg in het web. De spin neemt de kortste route naar de vlieg. Hoeveel meter moet hij dan afleggen? Iedere brugpieper weet dat je de stelling van Pythagoras nodig hebt om te berekenen hoe lang de schuine zijde is van een rechthoekige driehoek met zijden van (5+6) en 3 meter. Het antwoord lijkt dus: de wortel van de som van de kwadraten van 11 en 3, ofwel 11,4 meter. Helaas. De kortste route loopt grotendeels over de vloer van de kamer en is slechts 10 meter.
Leuk zijn ook de logische raadsels, zoals dat van de negen ringen. Op een tafel liggen negen ringen, die uiterlijk niet van elkaar te onderscheiden zijn. Slechts één ervan is echt, de andere zijn namaak. De echte ring is iets zwaarder. Hoe is het mogelijk om, met slechts twee keer wegen met een gelijkarmige balans, vast te stellen welke van de negen ringen de echte is?
Boekenwurm
Ook de raadsels over bewegende voorwerpen –„Jan en Piet fietsen allebei...”– ontbreken niet. Een klassieke instinker is die van de boekenwurm: een encyclopedie bestaat uit twee identieke delen van 600 bladzijden. De kaften zijn elk 5 millimeter dik, ieder blad papier is 0,1 millimeter dik en de delen staan in de kast naast elkaar zoals het hoort. Een boekenwurm kruipt vanaf pagina 1 van deel 1 in rechte lijn naar het midden van deel 2. Hoeveel millimeter legt hij af?
Het niveau van de raadsels is erg gevarieerd; ze staan lukraak door elkaar. Om frustratie te voorkomen, levert Ligtenberg bij zijn hersengymnastiek ook de oplossingen. Die nemen bijna evenveel bladzijden in als de raadsels zelf. Voor een aantal lastige problemen is er een speciale afdeling in het boek waarin alvast een tipje van de sluier wordt opgelicht – bedoeld voor degene die niet direct de pagina's met de oplossingen opslaat. Het boekje staat garant voor uren plezier en is vooral een aanrader voor wiskundedocenten of leiders van jeugdverenigingen.
Het aantal bladzijden van het boekje is groter dan het aantal opgaven; het is het kwadraat van een even getal; de som van de cijfers van het aantal bladzijden vormt ook een kwadraat, maar nu van een oneven getal. Rara... (het betreft hier het op het persbericht vermelde aantal bladzijden, in werkelijkheid zijn het er acht minder). N.a.v. ”De spin en de vlieg”, door H. Ligtenberg; uitg. Elmar, Rijswijk, 1999. ISBN 9038909284; ƒ 14,50.
